Chapter 5 パネルデータ分析
パネルデータ分析自体の解説はこちらからどうぞ。
5.1 検証する仮説
「当該路線上で市場集中度が高いほど、運賃は高くなるのでは?」という仮説を検証してみます。市場集中度を示す値として、今回の分析では各路線上でトップシェアを誇るエアラインの市場シェアを使って分析していきます。
5.2 データの読み込み
今回はexcel ファイルを読み込むので、openxlsxというパッケージに含まれているread.xlsx()関数を使います。
データを見てみます。データの1行は、各年度の各路線における情報が記載されています。つまり、年度ごとに各路線に関して観察したデータになっています。このように観察単位(路線)を複数の期間(年)で観察したデータをパネルデータといいます。
## year origin destin dist passen fare bmktshr
## 1 1997 "AKRON, OH" "ATLANTA, GA" 528 152 106 0.8386
## 2 1998 "AKRON, OH" "ATLANTA, GA" 528 265 106 0.8133
## 3 1999 "AKRON, OH" "ATLANTA, GA" 528 336 113 0.8262
## 4 2000 "AKRON, OH" "ATLANTA, GA" 528 298 123 0.8612
## 5 1997 "AKRON, OH" "ORLANDO, FL" 861 282 104 0.5798
## 6 1998 "AKRON, OH" "ORLANDO, FL" 861 178 105 0.5817
## ID
## 1 1
## 2 1
## 3 1
## 4 1
## 5 2
## 6 2○変数の説明
| 変数名 | 説明 |
|---|---|
| year | 年 |
| origin | 出発地 |
| destin | 到着地 |
| dist | 距離 |
| passen | 平均乗客数 |
| fare | 運賃 |
| bmktshr | 各路線上でトップシェアを誇るエアラインの市場シェア |
| ID | 路線に紐づけられたID |
5.3 データの把握
5.3.1 基本統計量
いつも通りのsummary()です。
## year origin destin
## Min. :1997 Length:4596 Length:4596
## 1st Qu.:1998 Class :character Class :character
## Median :1998 Mode :character Mode :character
## Mean :1998
## 3rd Qu.:1999
## Max. :2000
## dist passen fare
## Min. : 95.0 Min. : 2.0 Min. : 37.0
## 1st Qu.: 505.0 1st Qu.: 215.0 1st Qu.:123.0
## Median : 861.0 Median : 357.0 Median :168.0
## Mean : 989.7 Mean : 636.8 Mean :178.8
## 3rd Qu.:1304.0 3rd Qu.: 717.0 3rd Qu.:225.0
## Max. :2724.0 Max. :8497.0 Max. :522.0
## bmktshr ID
## Min. :0.1605 Min. : 1
## 1st Qu.:0.4650 1st Qu.: 288
## Median :0.6039 Median : 575
## Mean :0.6101 Mean : 575
## 3rd Qu.:0.7531 3rd Qu.: 862
## Max. :1.0000 Max. :11495.3.2 データの可視化
今回のモデルの被説明変数になるfareに関して可視化してみましょう。今回はggplot2()というパッケージを使ってみます。詳細はこちらのリンク集を参考にしてください。
ggplot()で可視化したいデータを指定して、その後可視化の手法(ヒストグラム、箱ひげ図、散布図…)を指定します。ヒストグラムを描きたい場合はgeom_histogram()です。
## `stat_bin()` using `bins = 30`. Pick better value with
## `binwidth`.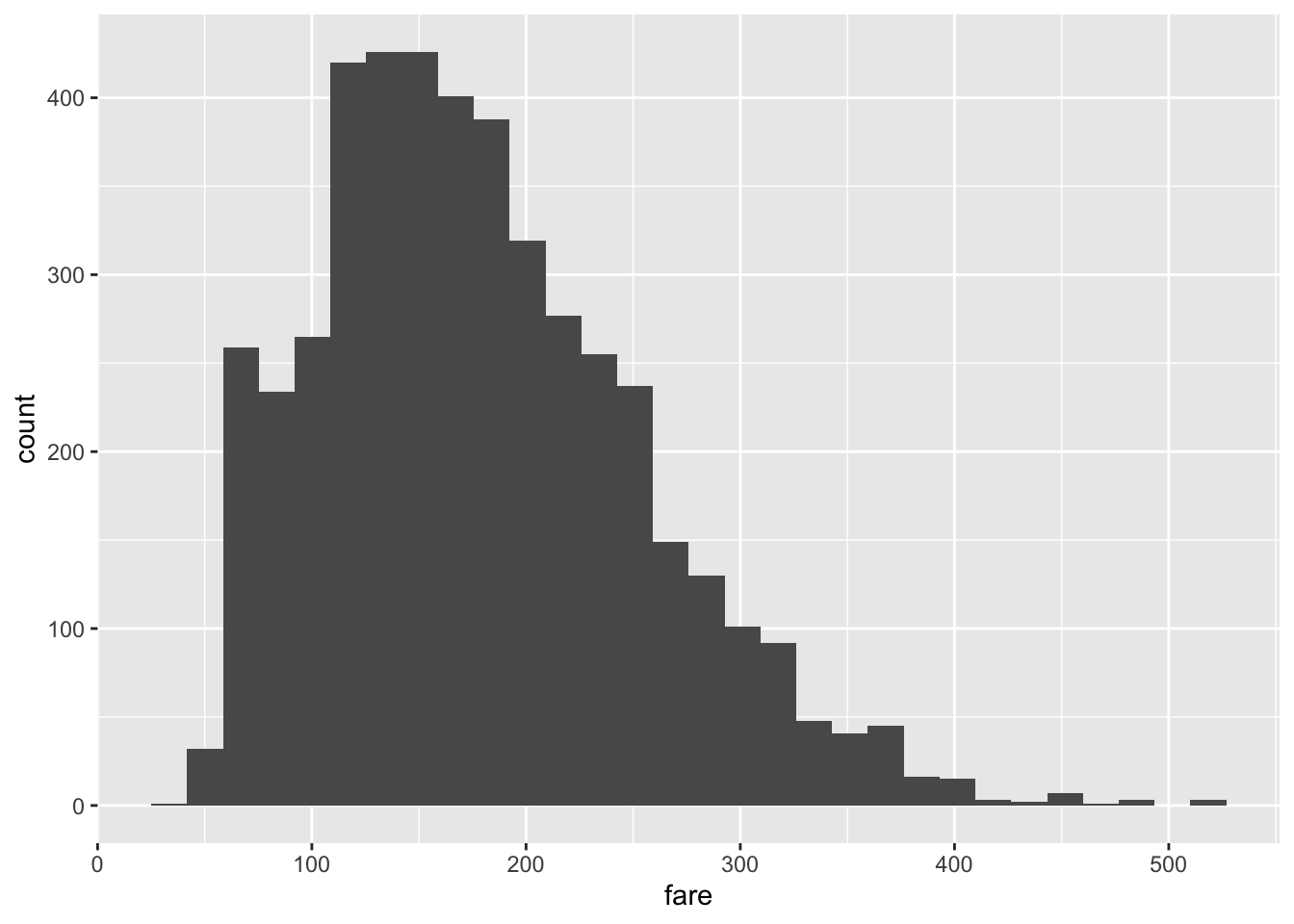
細かいオプションとしては、geom_histogram(binwidth = 10)のようにbinwidthでヒストグラムの幅を指定出来たりします。labs()ではグラフのタイトルやx軸, y軸の名前も指定出来ます。
g <- ggplot(df, aes(x = fare))
g <- g + geom_histogram(binwidth = 10)
g <- g + labs(title = "Histogram of fare")
plot(g)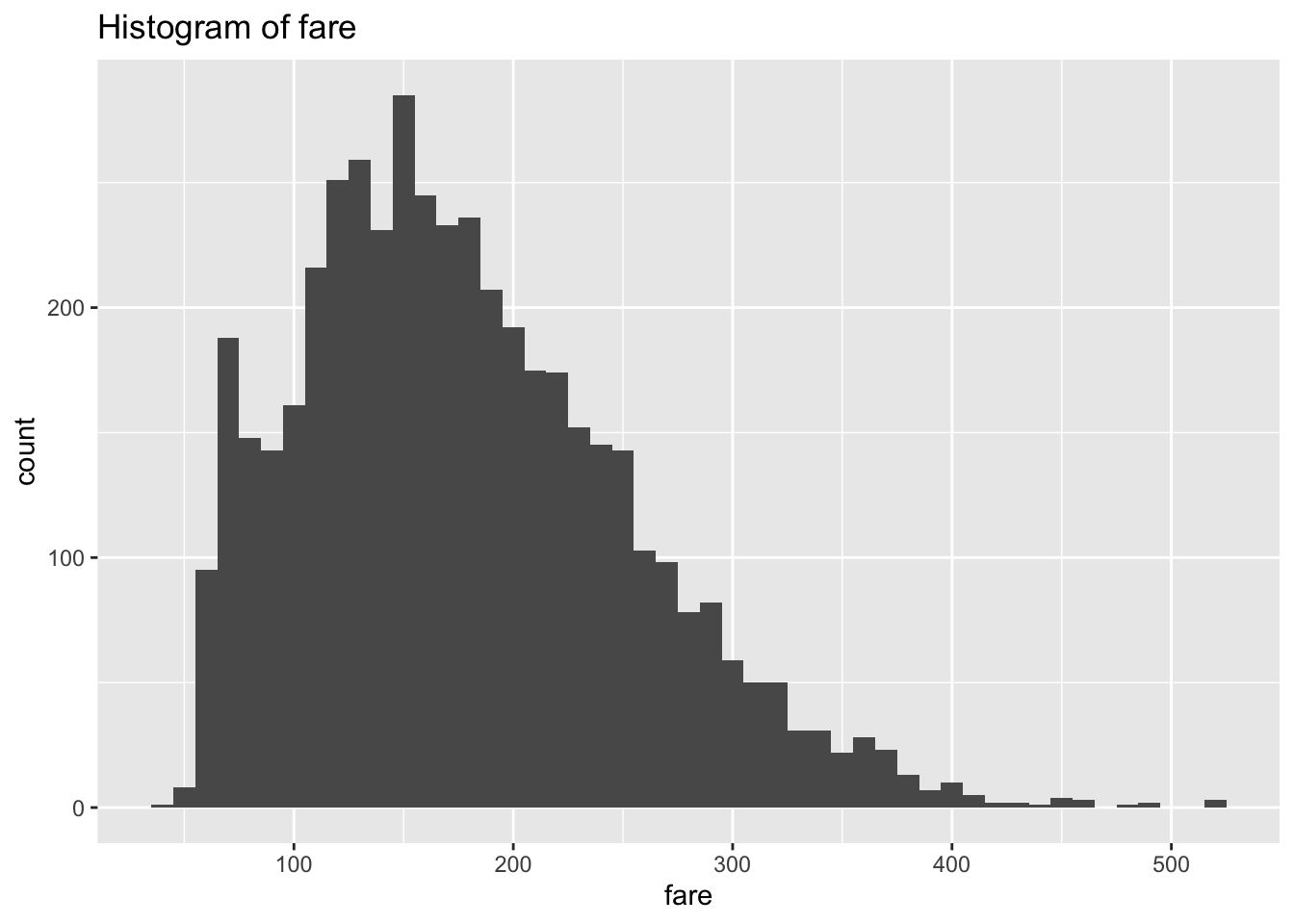
5.3.3 対数変換
運賃の分布は左側に偏っていますね。今回は対数に変換することで、この分布の歪みを解消させてみます。log()関数を使えば、簡単に対数に変換することが出来ます。対数をとると非線形の推定式を線形として解くことが出来たりするので、よく使います。
df$ln_fare <- log(df$fare)
g <- ggplot(df, aes(x = ln_fare))
g <- g + geom_histogram()
g <- g + labs(title = "Histogram of ln_fare")
plot(g)## `stat_bin()` using `bins = 30`. Pick better value with
## `binwidth`.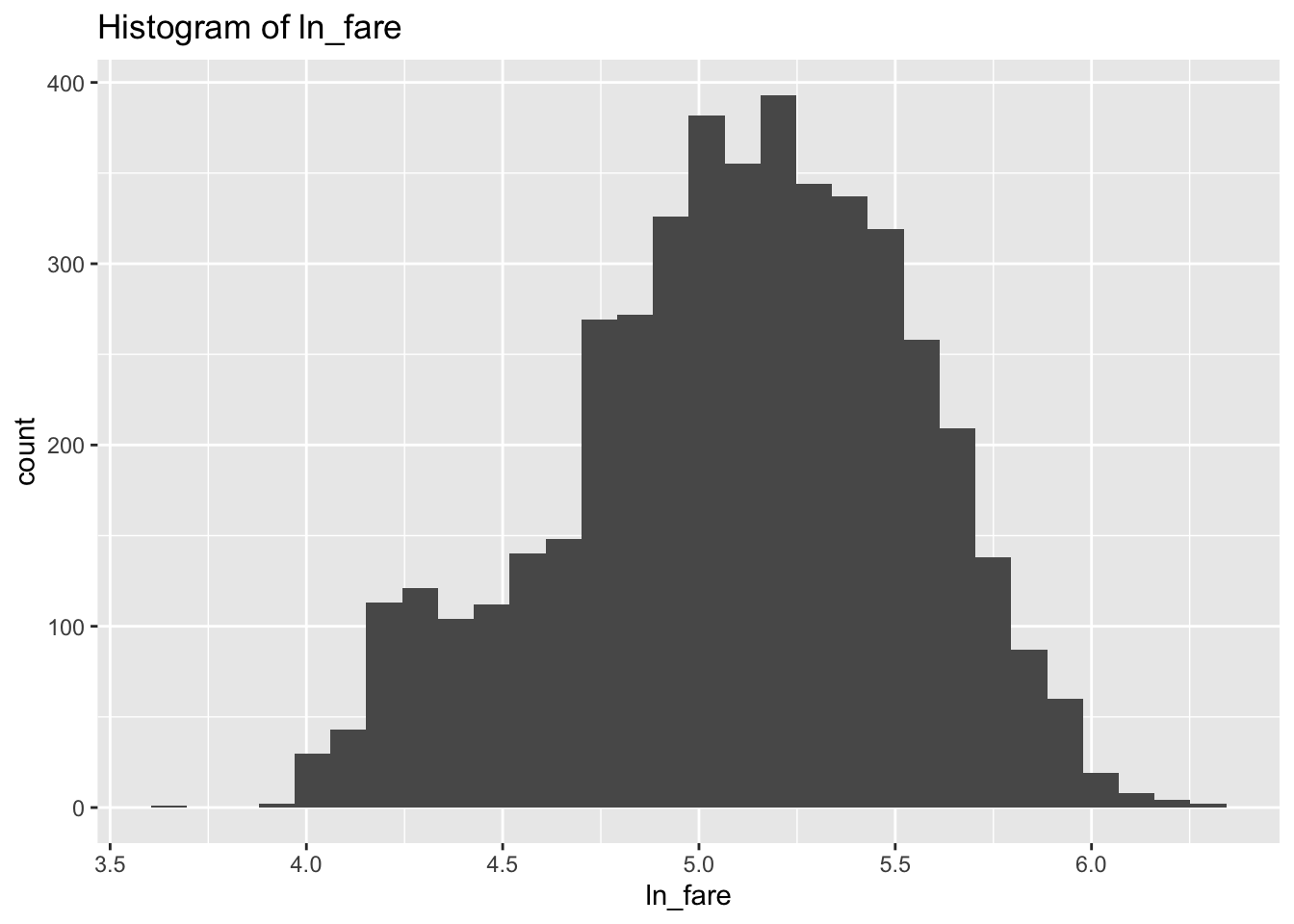
5.4 推定
5.4.1 計量経済学モデル
\(F=i\)は観察単位(路線)\(i\)の固有効果を示しています \[ ln\_fare_{i,t} = \alpha + \beta_{1}\times bmktshr_{i,t}+ \beta_{2}\times dist_{i,t}+ \beta_{3}\times passen_{i,t}+ F_i + u_{i,t} \]
5.4.2 準備
パネルデータ分析では、plmパッケージを使います。
Rにパネルデータであると認識させるために、pdata.frame()という関数を使います。()の中のindex()において、パネルデータの観察単位と期間を示す変数を指定します。
5.4.3 変量効果モデル
まずは、変量効果モデルで推定していきます。plm()関数の中で、model = "random"と指定するだけです。他はいつものlm()と同じ書き方です。
summary()で結果を見てみます。基本的に見方はいつも通りです。Balanced panelという項目が増えているくらいだと思います。
- Balanced panel
- n: 観察単位(路線)の数。
- T: 期間。今回は1997~2000なので、4です。
- N: サンプルサイズ
## Oneway (individual) effect Random Effect Model
## (Swamy-Arora's transformation)
##
## Call:
## plm(formula = ln_fare ~ bmktshr + dist + passen, data = df_panel,
## model = "random")
##
## Balanced Panel: n = 1149, T = 4, N = 4596
##
## Effects:
## var std.dev share
## idiosyncratic 0.01182 0.10871 0.103
## individual 0.10290 0.32078 0.897
## theta: 0.8329
##
## Residuals:
## Min. 1st Qu. Median 3rd Qu.
## -0.87882871 -0.06663365 -0.00065108 0.06643019
## Max.
## 0.89768536
##
## Coefficients:
## Estimate Std. Error z-value Pr(>|z|)
## (Intercept) 4.7083e+00 2.9902e-02 157.4573 < 2.2e-16 ***
## bmktshr 9.0534e-02 2.7385e-02 3.3059 0.0009466 ***
## dist 4.3095e-04 1.6696e-05 25.8108 < 2.2e-16 ***
## passen -1.4828e-04 9.6610e-06 -15.3481 < 2.2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Total Sum of Squares: 68.334
## Residual Sum of Squares: 56.06
## R-Squared: 0.17962
## Adj. R-Squared: 0.17908
## Chisq: 1005.39 on 3 DF, p-value: < 2.22e-165.4.4 固定効果モデル
次に固定効果モデルです。こちらはmodel = "within"です。
summary()で結果を見てみます。今回は固定効果モデルなので、期間で値が変化しないdist変数は固有効果に含まれてしまうので、結果から落とされています。
## Oneway (individual) effect Within Model
##
## Call:
## plm(formula = ln_fare ~ bmktshr + dist + passen, data = df_panel,
## model = "within")
##
## Balanced Panel: n = 1149, T = 4, N = 4596
##
## Residuals:
## Min. 1st Qu. Median 3rd Qu.
## -0.88515181 -0.04866045 -0.00023397 0.05151268
## Max.
## 0.95497340
##
## Coefficients:
## Estimate Std. Error t-value Pr(>|t|)
## bmktshr 0.02373293 0.03000237 0.791 0.429
## passen -0.00029409 0.00001540 -19.097 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Total Sum of Squares: 45.169
## Residual Sum of Squares: 40.716
## R-Squared: 0.098576
## Adj. R-Squared: -0.20234
## F-statistic: 188.365 on 2 and 3445 DF, p-value: < 2.22e-16固定効果自体はfixefで取り出せます。
## [1] 5.2684055.4.5 ハウスマン検定
ハウスマン検定は、変量効果モデルと固定効果モデルとで、どちらのモデルを選択するべきかに答えてくれます。p値が小さい値であれば、対立仮説である固定効果モデルが採択されます。phtest()に2つの推定モデルの結果を入れてあげます。
##
## Hausman Test
##
## data: ln_fare ~ bmktshr + dist + passen
## chisq = 157.91, df = 2, p-value < 2.2e-16
## alternative hypothesis: one model is inconsistent5.4.6 固定効果×時間効果
固有の効果に加えて、時間\(t\)ごとの効果もコントロールすることも出来ます。具体的には、ある特定の期間だけ石油の値段が上昇したために運賃が高くなった。といった効果をコントロールできるはずです。 \[ ln\_fare_{i,t} = \alpha + \beta_{1}\times bmktshr_{i,t}+ \beta_{2}\times dist_{i,t}+ \beta_{3}\times passen_{i,t}+ F_i +y\_1997_{i, t} +y\_1998_{i, t} +y\_1999_{i, t} + u_{i,t} \]
effect = "twoways"と指定するだけです。
out_fix_time <- plm(ln_fare ~ bmktshr+ dist + passen , data = df_panel, effect = "twoways", model = "within")
summary(out_fix_time)## Twoways effects Within Model
##
## Call:
## plm(formula = ln_fare ~ bmktshr + dist + passen, data = df_panel,
## effect = "twoways", model = "within")
##
## Balanced Panel: n = 1149, T = 4, N = 4596
##
## Residuals:
## Min. 1st Qu. Median 3rd Qu. Max.
## -0.819590 -0.035576 0.001385 0.037447 0.872410
##
## Coefficients:
## Estimate Std. Error t-value Pr(>|t|)
## bmktshr 8.3408e-02 2.6626e-02 3.1326 0.001747 **
## passen -4.0067e-04 1.4055e-05 -28.5066 < 2.2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Total Sum of Squares: 39.434
## Residual Sum of Squares: 31.6
## R-Squared: 0.19867
## Adj. R-Squared: -0.069759
## F-statistic: 426.68 on 2 and 3442 DF, p-value: < 2.22e-165.5 推定結果の整理
OLS推定もやっておきます。
結果をstargazerでまとめてみました。(1)式がOLS、(2)式が固定効果モデル、(3)式が変量効果モデル、(4)式が時間効果を考慮して固定効果モデルです。(4)式をみてみると、bmktshrの係数が有意に正となっているので、仮説は検証されています。ただ他にも運賃に影響を与える変数はありそうなので、データをリッチにしてコントロールしていく必要がありそうです。
##
## ================================================================================================================
## Dependent variable:
## --------------------------------------------------------------------------------------------
## ln_fare
## OLS panel
## linear
## (1) (2) (3) (4)
## ----------------------------------------------------------------------------------------------------------------
## bmktshr 0.261*** 0.024 0.091*** 0.083***
## (0.030) (0.030) (0.027) (0.027)
##
## dist 0.0005*** 0.0004***
## (0.00001) (0.00002)
##
## passen -0.0001*** -0.0003*** -0.0001*** -0.0004***
## (0.00001) (0.00002) (0.00001) (0.00001)
##
## Constant 4.508*** 4.708***
## (0.027) (0.030)
##
## ----------------------------------------------------------------------------------------------------------------
## Observations 4,596 4,596 4,596 4,596
## R2 0.396 0.099 0.180 0.199
## Adjusted R2 0.395 -0.202 0.179 -0.070
## Residual Std. Error 0.339 (df = 4592)
## F Statistic 1,002.387*** (df = 3; 4592) 188.365*** (df = 2; 3445) 1,005.385*** 426.680*** (df = 2; 3442)
## ================================================================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01